 |
PIAS Manual
2026
Program for the Integral Approach of Shipdesign
|
 |
PIAS Manual
2026
Program for the Integral Approach of Shipdesign
|
There are three types of subcompartments, as defined above. They can be used interchangeably at random, the use of different types of subcompartments within one compartment is also allowed. Although the user is entirely free to choose the type, there are still a few directions to be given:
Names of (sub)compartments, reference planes and physical planes can be 50 characters long, while all visible characters are allowed. Compartment names must be unique, which is not a basic requirement in itself, but in order to keep a compartment collection orderly it has been decided upon to require this. Names of physical planes need not be unique, it might occur that there are planes with different shapes, but that they are still at the same position, so one can give them the same name. It is doubtful whether this is practical, but that is up to the user. Reference planes have infinite dimensions, so there is no need to have planes at the same position, and it may therefore be required that their names are unique. Subcompartment names only matter within one compartment, so it is not necessary that they have a unique name. When copying a (sub)compartment or reference plane, the copy gets the name of the original with the addition ‘(copy)’. At least, if there is place left for that and when that name is not yet in use, otherwise the copy keeps its original name.
As mentioned at the definition of subcompartments, these can be positive or negative. It is not necessary, but a positive and a negative subcompartment are often used to model exactly the same space. For example, a fuel oil day tank in the ER as positive subcompartment, and exactly the same space as negative subcompartment which is deducted from the ER. It may be practical in such cases to define the shape of that subcompartment not twice, but only once, and to make a link to the second one. The advantage of this is that a geometry modification in one subcompartment is directly applied to the second one.
Such a link only applies to the shape and the name, not to the permeabilities (μ). There are sound reasons for that, because permeabilities may vary, like in our example where when the μ of the MK is 85%, that of the subcompartment to be deducted must also be 85%, because there would be more volume deducted than added. But the μ of the fuel oil day tank is of course 98% (or any other permability chosen by the user).
Subcompartments of the type ‘with coordinates’ and ‘space generated between planes’ can be defined beyond the hull shape, typically to plus or minus ∞ (which can be defined by typing a <I> resp. <-><I> instead of a number, from infinite). In that case, the intersections between subcompartment and hull shape are determined automatically. The hull shape itself can be defined through frames (with module Hulldef) or as solid model (with Fairway). In the latter case, an entire planes model of the hull is available with which any subcompartment intersection can be made. But in the event of a frame model, there are only frames, there is nothing in between. That does not matter at all, PIAS has (traditionally) sufficient methods to arithmetically find an adequate solution, but for drawing the program must be driven back on interpolation of a subcompartment plane with those frames. In case of a longitudinal plane, such as a deck or longitudinal bulkhead, there will be in general sufficient intersections between that plane and the frames, so that a sufficiently accurate intersection line can be drawn. But in the event of angled bulkheads it is very well possible that there are only a few intersections with the frames. In theory, the intersection line can be drawn on the basis of these intersections, but as their number is small, its accuracy can be low. There are two options here, the first one is to give a shrug, because we are only dealing with a picture and not with the calculation results, and the second one is a more complete definition by means of more frames, that can be quickly generated, for example, with Fairway.
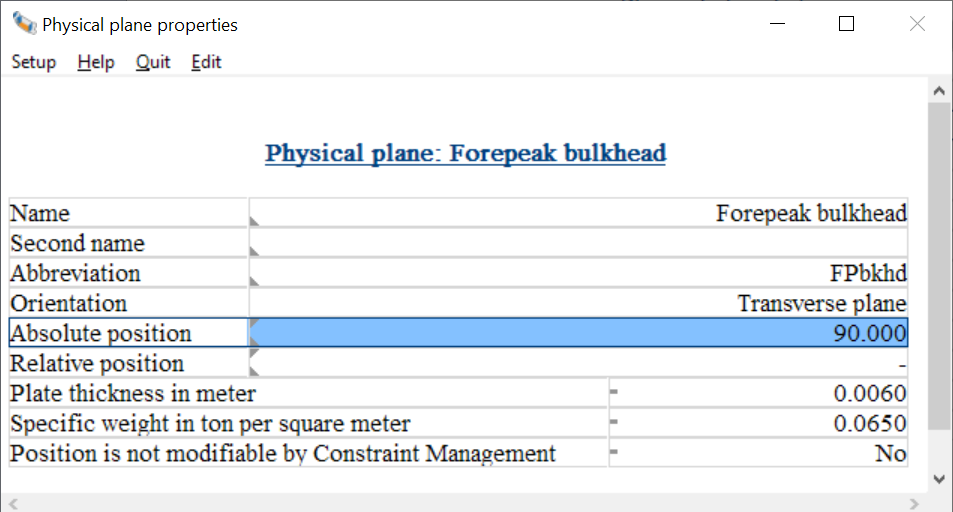
On multiple locations in Layout properties of a reference plane or a physical plane can be given in a text menu, from which an example is depicted above. Its parameters are the same as discussed in List of physical planes. If the <F5> function key is pressed on the cell ‘Absolute position’ or ‘Relative position’ then an extended menu with the plane geometry pops up, as discussed in the next paragraph.
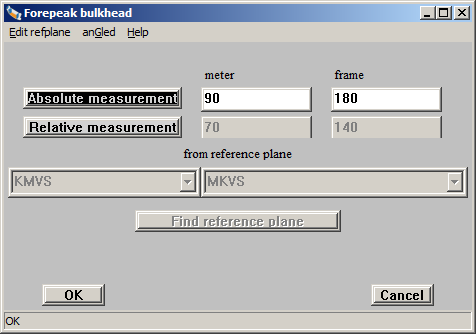
This menu is used to define the orientation, which is the direction and position, of a plane. Not only of a physical plane, but also of a reference plane. Here one can fill in:
Furthermore, this window consists of two functions in the upper bar:
| Enter | Next input field |
| Tab | Next input field |
| Shift Tab | Previous input field |
| Ctrl-A | Select everything in box |
| Ctrl-Del | Remove everything from box |
| Alt-O | OK |
| Alt-C | Cancel |
| Alt-R | Relative |
| Alt-A | Absolute |
| Alt-Z | Find reference plane |
| Alt-T | Transverse bulkhead (only applicable to a new plane) |
| Alt-L | Longitudinal plane (only applicable to a new plane) |
| Alt-D | Deck (only applicable to a new plane) |
So, this menu can be used to define the orientation of a plane, or to specify that a plane lies on a certain, fixed, distance from a reference plane. More or less the same menu is used to define points with respect to a reference plane. This popup menu is invoked by pressing <F5> in the cell with a coordinate of the point. Two more remarks ons reference planes:
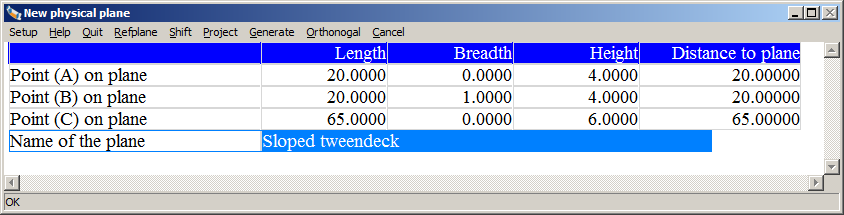
The orientation of an orthogonal plane, that is a transverse plane, longitudinal plane or horizontal plane, is entirely recorded with its type and one digit. In order to record an angled plane, however, more data are required. There are innumerable manners in which an angled plane can be recorded, but in Layout has been opted for doing this by means of three points in the space, because this is considered most intuitively. Those three points are in a menu, an example of which is given above. This menu essentially includes for any of the tree points a row, with in the columns the length, breadth and height coordinates of that point. As a matter of fact, these points are unrelated to any other point of the ship or its subdivsion — although the are fit to be linked to a reference plane. The last column contains the distance from that point to the angled plane. For the plane is not directly adjusted to the position of the three points, but for reasons of safety it has been chosen that the function [Generate] must be called upon there later on. Other functions that are available in the upper bar are:
The constellation of physical planes also fixes the nature and shape — or, put another way, the topology and geometry — of the enclosed spaces, the compartments. That's nice, but it also introduces a limitation because planes cannot be passed by their immediate neighbors; that would, after all, compromise the entire ‘logic’ of the subdivision. That can extent further than one might think at first glance, because planes can also indirectly (by means of reference planes) get a location. Thats all internally monitored in Layout, and if one would place a plane beyond its topological limit it is pushed back to its extreme limit. No warning is given on that — that might in fact lead to rather long warning lists, from which nobody benefits — but at least you now know the reason if a plane does not pass a certain location.
Around 1985 the PIAS module Compart was developed, for the definition of compartmentsm, calculations of tank tables etc. The current module Layout, which was developed in the years 2010-2012, serves the same purposes, but is much more extensive, for example because of the support with explicit decks and planes and a GUI. Compart files can be read in Layout, but this has to be done manually, see Import PIAS compartments from pre-2012 format. If, on the basis of these compartments, subsequently physical planes are being generated it may be useful to clean the compartments first, see Clean pre-2012 PIAS compartments.
More information on the purpose and operation of constraint management can be found here and here.
Constraint Management is restricted to address the constraint problem as far as it can be included in a processing time that allows interactivity. Currently only constraints that deal with plane positions, areas and compartment volumes are considered.
Constraints can be categorized by two distinct properties, that we call groups and types. The group the constraint belongs to says something about how the constraints relates to the geometry of the vessel. Four different groups are identified:
It is important to note that the group amount is present, but is purely a 'bookkeeping' tool. This is because the Constraint Management feature works by changing the position of the physical planes of the model. It can not actually create new geometry features.
The second property of a constraint is its type. This type conveys the meaning of the numerical value of the constraint. Four types are identified:
The input table for the constraints can be opened via the menu bar in the graphical user interface: cOnstraints -> edit constraints. A constraint is defined by a name and abbreviation, its group, type and the associated upper and/or lower limits. Lastly the constraint can be set to inactive to disregard it in the constraint evaluation step.
An example of a constraint table is shown below.
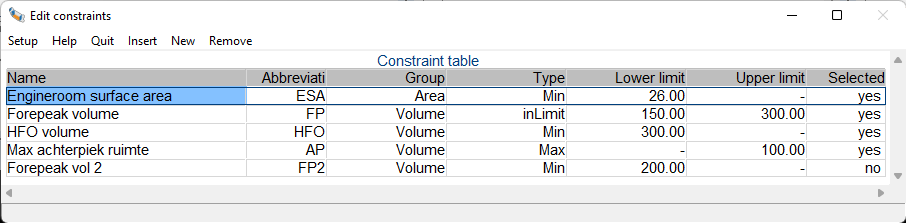
After a constraint has been created it needs to be coupled to its compartment or physical plane. This can be done by opening the compartment properties (see Number of constraints) or the physical plane properties (see List of physical planes), and then setting the number of constraints value to the desired amount. Then, for that number of constraints, a constraint from the constraint table can be selected.
An evaluation can be performed from the menu bar via cOnstraints->evaluate. Constraint management will attempt to find a solution that satisfies all active constraints.
As the various constraints probably require different things from the vessel, finding the right design compromise that satisfies all constraints can be a challenge. Often, not all the constraints are equally important, or they influence the design changes unequally and should thusly be weighted differently. Since the relative importance of the constraint is dependent not only on the specific constraint itself, but is also relative to the other active constraints in the model, the assigning of the relative importance to the active constraints is left to the user, in order to push the design in the direction that they desire.
By opening the constraint balance window the weights of the various active constraints that are linked to at least one compartment of physical plane can be set relative to each other. This can be done by the position of the slider in the vertical trackbar. Each trackbar is titled with the abbreviation of its constraint, the constraint type, and below are in order the set upper boundary value, the current value, and the lower boundary value. If the current value does not comply with the constraint it is printed in red for easy identification.
Below is an example of the constraint balance window:
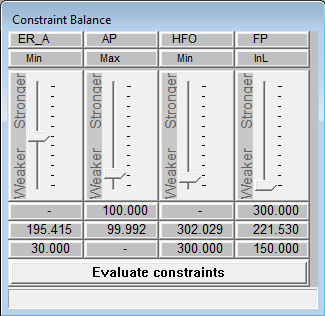
After the sliders of the constraints are set to the desired positions, the 'Evaluate constraints' button at the bottom of the constraint balance can be pushed to attempts to find a solution that satisfies all the constraints. This is done by moving all the physical planes in the model, except those that are set to not be modifiable by constraint manager. The solution is optimized for the smallest repositioning of the physical planes, so as to stay as close as possible to the designers intent when setting up the model.
Having started up Layout, one enters the main menu, the various options of which are explained in more detail in the following sections.