With this module properties can be computed from propellers of the following, published, empirical propeller series:

Open water propellers of the systematic B-series of MARIN, Wageningen, The Netherlands.
Ducted propellers of the systematic Ka-series, and one from the Kd-series of MARIN.
Propeller series by Gawn.
The Japanese Au series for three-bladed, four-bladed and six-bladed propellers.

Overview and applicability of the calculation methods

Note: Please take the warning in the note of Overview and applicability of the calculation methods. — on the attitude with respect to empirical/statistical prediction methods — heartily.

B-serie

The calculation is based on the methode of M. Oosterveld & P. van Oossanen, NSP 1974, and is valid for pitch/diameter ratios between 0.6 and 1.4. The applicable blade numbers and blade area ratios are listed in the table below:

Number of blades	2	3	4	5	6	7
Expanded area ratio	0.3	0.35-0.8	0.4-1.0	0.45-1.05	0.5-0.8	0.55-0.85

Ka/Kd-series

The calculation is based on the method of M. Oosterveld, ‘Ducted propeller characteristics’, RINA 1973, and is valid for pitch/diameter ratios between 0.5 and 1.6, and for the following propeller/nozzle combinations:

Propeller	Nozzel	Number of blades	Blade area ratio
Ka 3-65	19A	3	0.65
Ka 4-55	19A	4	0.65
Ka 4-70	19A	4	0.70
Ka 4-70	22	4	0.70
Ka 4-70	24	4	0.70
Ka 4-70	37	4	0.70
Ka 5-75	19A	5	0.75
Ka 5-100	33	5	1.00

The different nozzles have the following particulars, where L is the length of the nozzle and D the propeller diameter.

nozzle 19A - L/D = 0.5, accelerating flow type
nozzle 22 - L/D = 0.8, accelerating flow type
nozzle 24 - L/D = 1.0, accelerating flow type
nozzle 33 - L/D = 0.6, decelerating flow type
nozzle 37 - L/D = 0.5, accelerating flow type

Nozzle 22 and 24 are similar to 19A, except for the L/D ratio which is higher, which is favourable for tugs. Nozzle 37 has a thick trailing edge which results in better performance with power astern. Nozzle 33 has a higher cavitation limit which is favourable to decrease the level of vibrations and noise.

Gawn-series

The calculation is based on the method of R. Gawn, ‘Effect of pitch and blade width on propeller performance’, RINA 1952, and has the following application area:

Only 3 bladed propellers.
Expanded area ratio should be between 0.2 and 1.1.
Pitch/diameter ratio should be between 0.8 and 1.4.

AU-series

The calculation is based on the method of A. Yazaki, ‘Design diagrams of modern four, five, six and seven-bladed propellers developed in Japan’, 4^th Naval Hydronamics Symposium, National Academy of Sciences, Washington, 1962. The parameters should be within the following limits per propeller:

Propeller name	N-AU 3-35	N-AU 3-50	AU 4-55	AU 4-70	AUw 6-55	AUw 6-70	AUw 6-85
Number of blades	3	3	4	4	6	6	6
Expanded area ratio	0.35	0.5	0.55	0.7	0.55	0.7	0.85
Pitch/diameter ratio	0.4-1.2	0.4-1.2	1.0-1.6	1.0-1.6	0.9-1.5	0.9-1.5	0.9-1.5

Main menu

Propeller calculations

1.	Input of ship hull parameters
2.	Input of propeller data
3.	Input of speed and resistance range
4.	Calculate propeller with maximum efficiency in a range of diameters
5.	Calculate propeller with revolutions variation
6.	Calculate resistance with fixed propeller dimensions
7.	Calculate speed-power curve with fixed propeller dimensions
8.	Calculate thrust force for a fixed pitch propeller
9.	Calculate thrust force for a controlable pitch propeller
10.	Local cloud monitor
11.	File and backup management

Input of ship hull parameters

Here an input window with ship hull parameter appears. Excepts for the drafts, they will only be utilized for the estimation of wake and thrust deduction coefficients (by Holtrop & Mennens method), not for the propeller calculations as such. If the resistance values have been transferred from Resistance to Propeller, those parameters are already filled in, because they have already been defined in Resistance and have been cotransferred. So, for their description reference is made to Input data resistance prediction.

Input of propeller data

Number of propellers: 1 or 2, so, single screw or twin screw propulsion. With two propellers, all over the computations the presence of two propellers are taken into account, and the final resulting shaft power applies obviously to the entire vessel, not for a single propeller.
Number of blades per propeller will speak for itself. The minimum or maximum number depends on the selected propeller series.
Losses in propeller axis: mechanical loss in percent.
Diameter start-increment-end can be specified in order to make calculations for a series of propeller diameters.
revolutions start-increment-end is specified to make calculations for a range of propeller revolutions. However, this is only used in calculation 5.
Pitch/diameter ratio: the pitch/diameter ratio has to be filled in by calculations 6 and 7. With calculation 4 and 5 this value is determined by the program.
Determination center shaft - base: if this option is set ‘0.53 × diameter’ then the distance between the center of the propeller shaft and baseline is recalculated for each diameter (with this = 53% of the propeller diameter). If the option is set to ‘User defined’ than the user-specified value is used.
Expanded area ratio: the expanded area ratio (A_E/A₀) of the B-series and Gawn propellers can be estimated by the program (according to the cavitation criterion of Keller) by setting the field ‘Determination method blade-area ratio’ to ‘Calculate’.
Wake and thrust deduction: There are three methods:
- Estimate according Holtrop & Mennen: with this estimation method (see Resistance for the references) on basis of the ship hull parameters, like defined in the first menu option(see Input of ship hull parameters), the wake and thrust deduction is estimated. If this method is not used, then these ship hull parameters (except for the drafts) no not neccessarily have to be given.
  Unfortunately, experience has shown that for full single-propeller vessels the Holtrop & Mennen formulae tend towards unrealistic high values. In such as case — higher than the tentatively selected wake factor of 0.45 — an alternative formula is used, namely that of Schneekluth (1988). This is a bit of a ramshackle, but that is not uncommon with empirical estimation methods.
- Fixed, user-specified values: Here you defined one wake and thrust deduction which will be used for every speed and diameter.
- User defined per speed-diameter: In this menu the wake and thrust deduction can be defined per speed-diameter. If changes are made to the number of speeds-diameters than you have to check if these user defined wake and thrust deduction values are still valid for there respective speed-diameter combination.
Propeller series: The to be used propeller series. With the Ka- and AU-series the following input parameters are automatically determined in and cannot be changed:
- The number of blades.
- The expanded area ratio.
- The type of propeller.

Input of speed and resistance range

In this input screen you can enter up to twenty speeds with the resistance. Enter the speed in knots and resistance in KN.

Calculate propeller with maximum efficiency in a range of diameters

This option is for calculating a propeller at a given speed and resistance when the number of revolutions and the pitch of the propeller is unknown. The determined propeller has a maximum possible open water efficiency.

Calculate propeller with revolutions variation

This option calculates a propeller at a given speed, resistance and (range of) number of revolutions. The pitch is determined so that the delivered shaft horse power equals the required shaft horse power. The previous calculation option (maximum efficiency) calculates all combinations of speed and diameter. The present revolutions variation does, however, its calculations only for the very first diameter.

Calculate resistance with fixed propeller dimensions

This option is to determine the resistance at the trial trip. All propeller characteristics have to be defined by the user. Using the defined propeller dimensions the resistance is calculated.

Calculate speed-power curve with fixed propeller dimensions

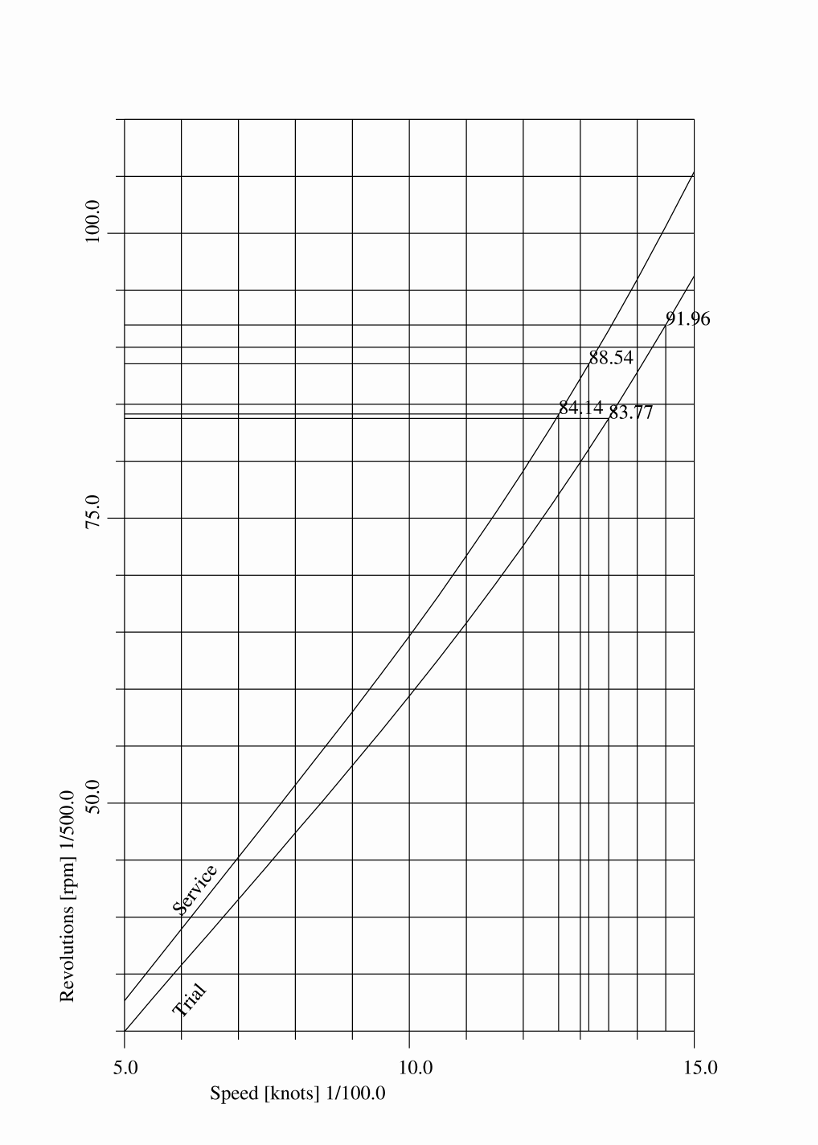
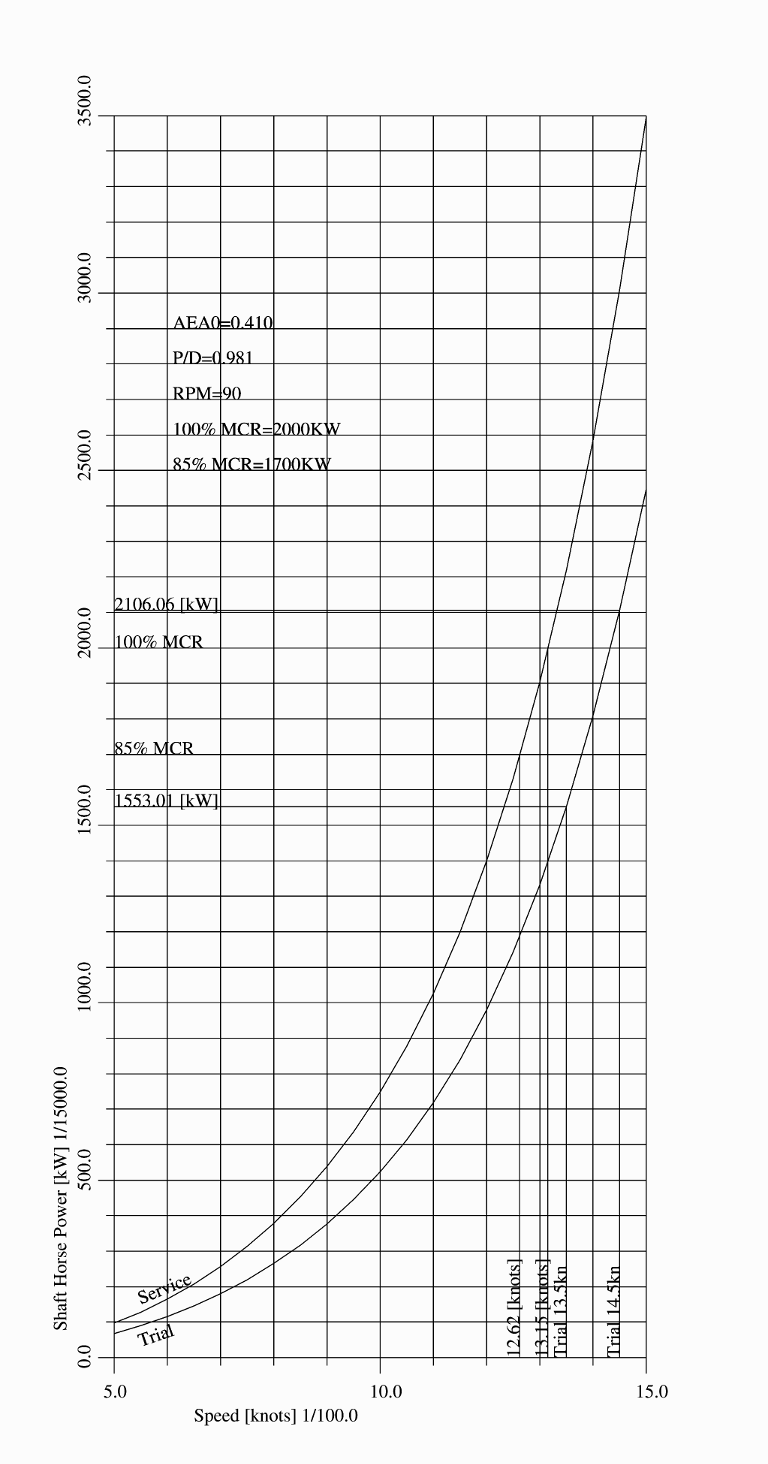
The following menu will be displayed on the screen, where with the first two options the speed-power curve is actually computed and plotted. The first option is for a fixed pitch propeller (and consequently varying revolutions), and the second for a controlable pitch propeller, with fixed revolutions. The other options can be used to configure the nature and content of the graph.

Speed-power curve for a fixed propeller dimensions

1.	Speed-power curve for a fixed pitch propeller
2.	Speed-power curve for a controlable pitch propeller
2.	Legends at the graph
3.	Allowances
4.	Efficiency reduction at constant revolutions
5.	Intersections in the graph
6.	Layout

For a propeller with fixed dimensions a graph can be plotted, which gives the relationship between the speed and the required shaft horse power. With the standard version the calculation can be performed for a fixed pitch propeller. The graphical extensions also allow calculations with a controllable pitch propeller. If there are any losses due to pitch variation, these can be defined by an allowance on the required power. The graph shows the shaft power at the speeds you specify. It is therefore important to specify sufficient speeds, with a small interval to obtain a smooth graph. Below you will find an example of such a graph.

Power curve.

Power curve with generated text labels.

Calculate thrust force for a fixed pitch propeller

With this option the thrust force can be calculated for a range of speeds, by varying the revolutions. The available shaft power (in KW) is defined at option 3, by entering the power instead of resistance. If the speed is zero, the wake factor and the thrust deduction fraction are default set to 0.05. This value can be changed by entering the wake and thrust factors by hand. The thrust force at speed zero is the bollard pull. The calculated thrust force reduced with the resistance, at speeds larger than zero, results in the available thrust force, for example for towing fishing gear.

Calculate thrust force for a controlable pitch propeller

With this option the thrust force can be calculated for a range of speeds, by varying the pitch-diameter ratio, for a fixed number of revolutions (for which the first revolutions value is taken from the range as given in option 2 ( Input of propeller data. Also for this option the shaft power should be given at option 3, by entering it (in KW) in the ‘Resistance’ column. For wake and thrust deduction factors, as well as bollard pull — the same remarks as from the previous option apply.

Local cloud monitor

This option pops up a window with a power curve, as discussed in Calculate speed-power curve with fixed propeller dimensions. However, here, in cloud context, this diagram is dynamic, which means it is recomputed and redrawn every time when data in the cloud which affects the power results changes. For more information on the cloud reference is made to Local cloud: simultaneous multi-module operation on the same project.

File and backup management

With this option design version can be managed, with a mechanism as described in Data storage and backups.